search

 search

Introduction to search

In computer science, a search data structure is any data structure that allows the efficient retrieval of specific items from a set of items, such as a specific record from a database.

The simplest, most general, and least efficient search structure is merely an unordered sequential list of all the items. Locating the desired item in such a list, by the linear searchmethod, inevitably requires a number of operations proportional to the number n of items, in the worst case as well as in the average case. Useful search data structures allow faster retrieval; however, they are limited to queries of some specific kind. Moreover, since the cost of building such structures is at least proportional to n, they only pay off if several queries are to be performed on the same database (or on a database that changes little between queries).

Static search structures are designed for answering many queries on a fixed database; dynamic structures also allow insertion, deletion, or modification of items between successive queries. In the dynamic case, one must also consider the cost of fixing the search structure to account for the changes in the database.

Types of search

v Linear search

v Binary search

v Jump search

v Interpolation search

v Exponential search

v Sublist search

v Fibonacci search

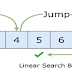
Jump Search

Jump search algorithm, also called as block search algorithm. Only sorted list of array or table can alone use the Jump search algorithm. In jump search algorithm, it is not at all necessary to scan every element in the list as we do in linear search algorithm. We just check the R element and if it is less than the key element, then we move to the R + R element, where all the elements between R element and R + R element are skipped. This process is continued until R element becomes equal to or greater than key element called boundary value. The value of R is given by R = sqrt(n), where n is the total number of elements in an array. Once the R element attain the boundary value, a linear search is done to find the key value and its position in the array. It must be noted that in Jump search algorithm, a linear search is done in reverse manner that is from boundary value to previous value of R.

Algorithm

Imagine you are given a sorted array, and you are applying linear search to find a value. Jump Search is an improvement to this scenario. Instead of searching one-by-one, we search k-by-k. Let’s say we have a sorted array A, then jump search will look at A[1], A[1 + k], A[1 + 2k], A[1 + 3k] … and so on.

As we keep jumping, we keep a note of the previous value and its index. Once we get a situation where A[i] < searchValue < A[i + k], then it means the value we want is in between the previous jump ends. So now we could simply perform a linear search between that A[i] and A[i + k].

Jump search implements using data structure
#include <bits/stdc++.h>

using namespace std;

 int jumpSearch(int arr[], int x, int n)a

{

    int step = sqrt(n);

    int prev = 0;

    while (arr[min(step, n)-1] < x)

    {

        prev = step;

        step += sqrt(n);

        if (prev >= n)

            return -1;

    }

    while (arr[prev] < x)

    {

        prev++;

        if (prev == min(step, n))

            return -1;

    }

    if (arr[prev] == x)

   return prev;

 return -1;

}

int main()

{

    int arr[] = { 0, 1, 1, 2, 3, 5, 8, 13, 21,

                 34, 55, 89, 144, 233, 377, 610 };

    int x = 55;

    int n = sizeof(arr) / sizeof(arr[0]);

    int index = jumpSearch(arr, x, n);

   cout << "\nNumber " << x << " is at index " << index;

    return 0;

}

 Output:-

Number 55 is at index 10

Exponential search

An exponential search (also called doubling search or galloping search or Struzik search) is an algorithm, created by Jon Bentley and Andrew Chi-Chih Yao in 1976, for searching sorted, unbounded/infinite lists. There are numerous ways to implement this with the most common being to determine a range that the search key resides in and performing a binary search within that range. This takes O(log i) where i is the position of the search key in the list, if the search key is in the list, or the position where the search key should be, if the search key is not in the list.

Exponential search can also be used to search in bounded lists. Exponential search can even out-perform more traditional searches for bounded lists, such as binary search, when the element being searched for is near the beginning of the array. This is because exponential search will run in O(log i) time, where i is the index of the element being searched for in the list, whereas binary search would run in O(log n) time, where n is the number of elements in the list

Algorithm

Exponential search allows for searching through a sorted, unbounded list for a specified input value (the search "key"). The algorithm consists of two stages. The first stage determines a range in which the search key would reside if it were in the list. In the second stage, a binary search is performed on this range. In the first stage, assuming that the list is sorted in ascending order, the algorithm looks for the first exponent, j, where the value 2j is greater than the search key. This value, 2j becomes the upper bound for the binary search with the previous power of 2, 2j - 1, being the lower bound for the binary search

template <typename T>

int exponential_search(T arr[], int size, T key)

{

    if (size == 0) {

        return NOT_FOUND;

    }

   int bound = 1;

    while (bound < size && arr[bound] < key) {

        bound *= 2;

    }

   return binary_search(arr, key, bound/2, min(bound, size));

}

Exponential search implements using data structure

#include <bits/stdc++.h>

using namespace std;

 int binarySearch(int arr[], int, int, int);

int exponentialSearch(int arr[], int n, int x)

{

    if (arr[0] == x)

        return 0;

    int i = 1;

    while (i < n && arr[i] <= x)

        i = i*2;

    return binarySearch(arr, i/2, min(i, n), x);

}

int binarySearch(int arr[], int l, int r, int x)

{

    if (r >= l)

    {

        int mid = l + (r - l)/2

        if (arr[mid] == x)

            return mid;

        if (arr[mid] > x)

            return binarySearch(arr, l, mid-1, x);

        return binarySearch(arr, mid+1, r, x);

    }

    return -1;

}

int main(void)

{

   int arr[] = {2, 3, 4, 10, 40};

   int n = sizeof(arr)/ sizeof(arr[0]);

   int x = 10;

   int result = exponentialSearch(arr, n, x);

   (result == -1)? printf("Element is not present in array")

                 : printf("Element is present at index %d",

                                                    result);

   return 0;

}

Output :

Element is present at index 3

Interpolation search

Interpolation search is an algorithm for searching for a given key in an indexed array that has been ordered by numerical values assigned to the keys (key values). It parallels how humans search through a telephone book for a particular name, the key value by which the book's entries are ordered. In each search step it calculates where in the remaining search space the sought item might be, based on the key values at the bounds of the search space and the value of the sought key, usually via a linear interpolation. The key value actually found at this estimated position is then compared to the key value being sought. If it is not equal, then depending on the comparison, the remaining search space is reduced to the part before or after the estimated position. This method will only work if calculations on the size of differences between key values are sensible.

Algorithm for Interpolation search

rest of the interpolation algorithm is same except the above partition logic.

Step1 :- In a loop,calucate the value of “pos” using the probe position formula.

step 2:-If a match,return the index of the item,and exit.

Step 3:-If the item is less than arr[pos],calculate the probe position of the left sub-array.otherwise the calculate the same in the right sub-array

Step 4:- Repeat until a match is found or the sub array reduces to zero.

Interpolation search implements using data structure
#include<stdio.h>

int interpolationSearch(int arr[], int n, int x)

{

    int lo = 0, hi = (n – 1);

    while (lo <= hi && x >= arr[lo] && x <= arr[hi])

    {

        int pos = lo + (((double)(hi-lo) /

              (arr[hi]-arr[lo]))*(x - arr[lo]));

        if (arr[pos] == x)

            return pos;

        if (arr[pos] < x)

            lo = pos + 1;

 else

        hi = pos - 1;

    }

    return -1;

}

void  main()

{

    int arr[] =  {10, 12, 13, 16, 18, 19, 20, 21, 22, 23,

                  24, 33, 35, 42, 47};

    int n = sizeof(arr)/sizeof(arr[0]);

    int x = 18;

    int index = interpolationSearch(arr, n, x);

    if (index != -1)

        printf("Element found at index %d", index);

    else

        printf("Element not found.");

    getch();

}

                   

 Output:-

             Element found at index 4

INDEXED SEARCH

Indexing is a way to optimize performance of a database by minimizing  the number os disk accesses required when a query is processed . An index or database index is a data structure  which is used to quickly locate and access

the in a data base table

Indexes are created using some database columns

·        The First column is the search key that contains a copy of the primary key or condiate key of the table these values are sorted in sorted order so that the corresponding data can be accessed quickly (note that the data may or may not be stored in sorted order ).

·        The  Second column is the data reference which contains a set of pointers holding the address of the disk block where that particular key value can be found .

Algorithm

In this section we will describe the algorithm for merge of inverted lists which is based on the index structure outlined in the previous section. We denote this special variant of B-tree as SB-tree in following. Let P(w, t) be a predicate: word w is contained in a document t. We consider queries of the following form: find all documents t, where ∧n i=1 ∨mi j=1 P(wij , t). Let Q = ∪n i=1 ∪mi j=1 wij be a set of all terms that occurs in the query. For query evaluation we use |Q| stacks which elements are SBtree entries contained in increasing order of text numbers. The entries of the leaf level nodes are placed into stacks in decoded form: (elem, elem, 0, NULL), where elem is a text number, dead space is zero and pointer to child node is null. The stacks are referred in the algorithm in two forms: Stack(i) i = 1,..., |Q| and Stack(wij ), so that if wij is k-th element in Q then Stack(k) and Stack(wij ) denote the same stack. Besides, we use one additional stack P osZones for storing extents showing zones of possible resulting document numbers. Now we describe the merge algorithm.s

Indexed search implements using   data structure

#include<stdio.h>
#include <conio.h>

#define MAX 10

structmainfile
{

intempid;
charname[25];
floatbasic;
};

struct indexfile

intindex_id;
int kindex;
};

void main()
{
struct mainfile fobj[MAX];
struct indexfile index[MAX];
int i,num,low,high,ct=4;
float basicsal;
clrscr();
for(i=0;i<MAX;i++)
{

printf(“\nEnter employee id?”);
scanf(“%d”,&fobj[i].empid);
printf(“\nEnter name?”);
scanf(“%s”,fobj[i].name);
printf(“\nEnter basic?”);
scanf(“%f”,&basicsal);
fobj[i].basic=basicsal;
}
printf(“\nNow creating index file…!”);
for(i=0;i<(MAX/5);i++)
{index[i].index_id=fobj[ct].empid;
index[i].kindex = ct;

ct=ct+5;
}

printf(“\n\nEnter the empid to search?”);
scanf(“%d”,&num);
for(i=0;(i<MAX/5) && (index[i].index_id<=num);i++)
low=index[i-1].kindex;
high=index[i].kindex;
for(i=low;i<=high;i++)
{if(num==fobj[i].empid)
{
printf(“\nThe record is: \n\t”);
printf(“\nEmpid: %d”,fobj[i].empid);
printf(“\nName: %s”,fobj[i].name);
printf(“\nBasic: %f”,fobj[i].basic);
getch();
return;
}
}
printf(“\nNumber not found…!”);
return;
}